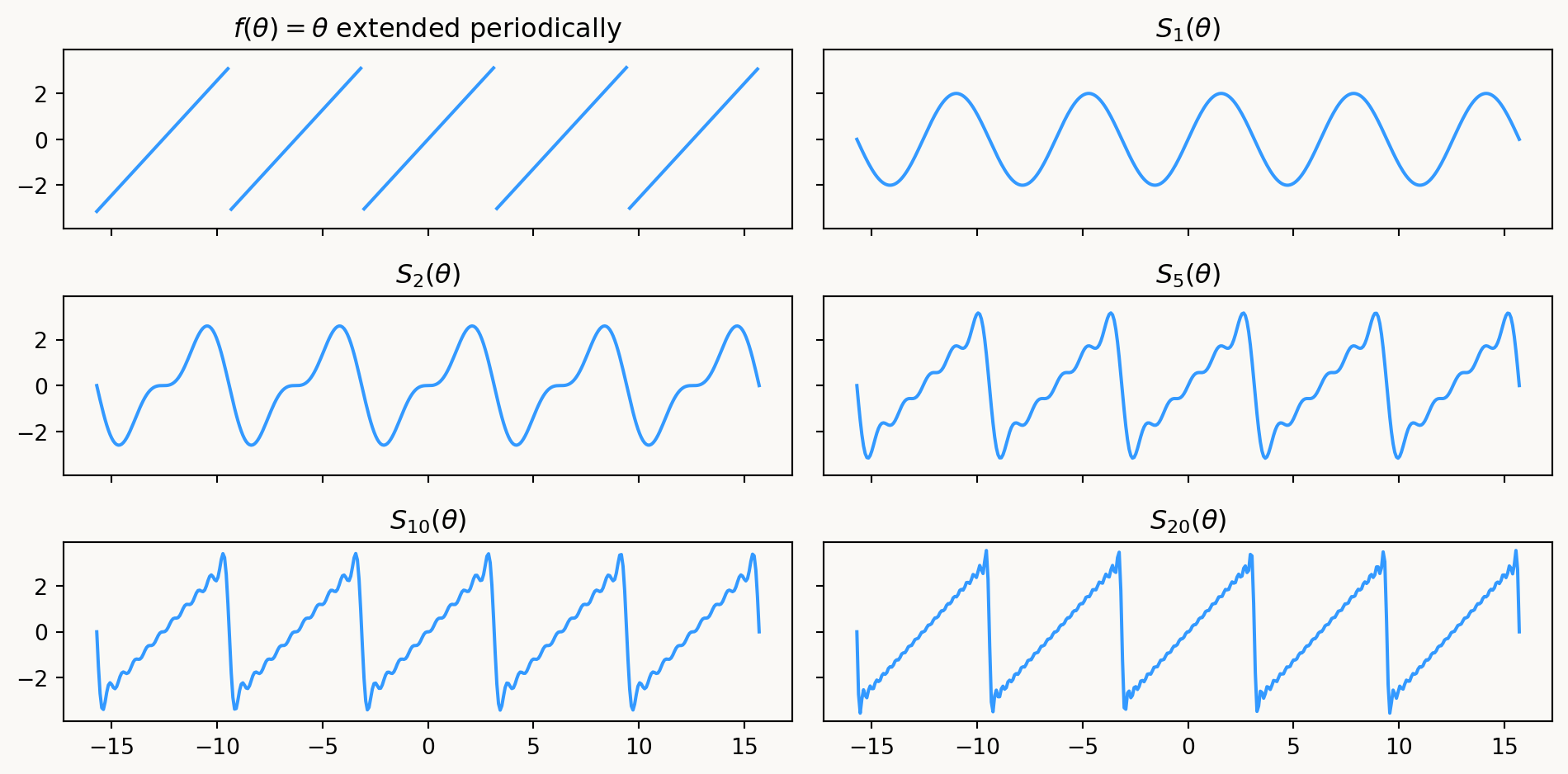
06 A first look at Fourier series, part 2

Exercise 1: Computing another Fourier series

Define the function \(f(\theta) = \theta\) for \(\theta \in [-\pi, \pi]\), and extend it to a function on \(\mathbb{R}\) with period \(2\pi\). Compute the Fourier coefficients and series of \(f\).

Bessel’s inequality: statement

Theorem (Bessel’s inequality — \(c\)-version).

If \(f:\mathbb{R} \to \mathbb{C}\) is a \(2\pi\)-periodic function, integrable on \([-\pi, \pi]\), and if \(c_n\) are its Fourier coefficients, then

\[ \sum_{n=-\infty}^\infty |c_n|^2 \leq \frac{1}{2\pi} \int_{-\pi}^\pi |f(\theta)|^2 \, d\theta. \]

Bessel’s inequality: context

For the moment, consider a familiar column vector, say in \(\mathbf{x} \in \mathbb{C}^3\) for simplicity: \[ \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}. \]
If we consider the standard basis vectors \[ \mathbf{e}_1 = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}, \quad \mathbf{e}_2 = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}, \quad \mathbf{e}_3 = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}, \] then can consider the three inner products (dot products): \[ \langle \mathbf{x}, \mathbf{e}_1 \rangle = x_1, \quad \langle \mathbf{x}, \mathbf{e}_2 \rangle = x_2, \quad \langle \mathbf{x}, \mathbf{e}_3 \rangle = x_3. \]
Then we obviously have \[ \sum_{n=1}^3 |\langle \mathbf{x}, \mathbf{e}_n \rangle|^2 = |x_1|^2 + |x_2|^2 + |x_3|^2 = \|\mathbf{x}\|^2. \]
In particular, we have \[ \sum_{n=1}^3 |x_n|^2 = \sum_{n=1}^3 |\langle \mathbf{x}, \mathbf{e}_n \rangle|^2 \leq \|\mathbf{x}\|^2. \]

Bessel’s inequality: more context

Now, consider two functions \(f,g: \mathbb{R} \to \mathbb{C}\) that are \(2\pi\)-periodic and integrable on \([-\pi, \pi]\). Suppose we define an inner product on such functions by \[ \langle f, g \rangle = \frac{1}{2\pi} \int_{-\pi}^\pi f(\theta) \overline{g(\theta)} \, d\theta. \]
Then, in complete analogy with the case of column vectors, it is natural to define \[ \|f\|^2 = \langle f, f \rangle = \frac{1}{2\pi} \int_{-\pi}^\pi |f(\theta)|^2 \, d\theta. \]
Notice also that \[ \langle f, e^{in\theta} \rangle = \frac{1}{2\pi} \int_{-\pi}^\pi f(\theta) e^{-in\theta} \, d\theta = c_n, \] for each integer \(n\).
In other words, the Fourier coefficients of \(f\) are precisely the inner products of \(f\) with the complex exponentials \(e^{in\theta}\).
From the previous slide, we have \[ \sum_{n=1}^3 |x_n|^2 = \sum_{n=1}^3 |\langle \mathbf{x}, \mathbf{e}_n \rangle|^2 \leq \|\mathbf{x}\|^2. \]
Arguing by analogy, we might expect that \[ \sum_{n=-\infty}^\infty |c_n|^2 = \sum_{n=-\infty}^\infty |\langle f, e^{in\theta} \rangle|^2 \leq \|f\|^2 = \frac{1}{2\pi} \int_{-\pi}^\pi |f(\theta)|^2 \, d\theta, \] which is precisely Bessel’s inequality.
In fact, in the case of column vectors, we have an equality, which suggests by analogy that (maybe?) we have an equality in the case of functions as well. This is indeed the case!

Bessel’s inequality: proof

Theorem (Bessel’s inequality — \(c\)-version).

If \(f:\mathbb{R} \to \mathbb{C}\) is a \(2\pi\)-periodic function, integrable on \([-\pi, \pi]\), and if \(c_n\) are its Fourier coefficients, then

\[ \sum_{n=-\infty}^\infty |c_n|^2 \leq \frac{1}{2\pi} \int_{-\pi}^\pi |f(\theta)|^2 \, d\theta. \]

Begin with the basic observation that \(|z|^2 = z \overline{z}\) for any complex number \(z\).
Applying this to \(z = f(\theta) - \sum_{n=-N}^N c_n e^{in\theta}\), we have \[ \left| f(\theta) - \sum_{n=-N}^N c_n e^{in\theta} \right|^2 = \left( f(\theta) - \sum_{n=-N}^N c_n e^{in\theta} \right) \overline{\left( f(\theta) - \sum_{n=-N}^N c_n e^{in\theta} \right)} = \left( f(\theta) - \sum_{n=-N}^N c_n e^{in\theta} \right) \left( \overline{f(\theta)} - \sum_{n=-N}^N \overline{c_n} e^{-in\theta}\right). \]
Expanding the right-hand side, we have \[ \left| f(\theta) - \sum_{n=-N}^N c_n e^{in\theta} \right|^2 = |f(\theta)|^2 - \sum_{n=-N}^N c_n \overline{f(\theta)} e^{in\theta} - \sum_{n=-N}^N \overline{c_n} f(\theta) e^{-in\theta} + \sum_{n=-N}^N \sum_{m=-N}^N c_n \overline{c_m} e^{i(n-m)\theta}. \]
Divide both sides by \(2\pi\), integrate from \(-\pi\) to \(\pi\), and recall that: \[ \frac{1}{2\pi} \int_{-\pi}^\pi f(\theta) e^{-in\theta} \, d\theta = c_n, \quad \text{and} \quad \frac{1}{2\pi} \int_{-\pi}^\pi e^{i(n-m)\theta} \, d\theta = \begin{cases} 1 & : n=m, \\ 0 & : n \neq m. \end{cases} \]
We get \[ \begin{align*} \frac{1}{2\pi} \int_{-\pi}^\pi \left| f(\theta) - \sum_{n=-N}^N c_n e^{in\theta} \right|^2 \, d\theta &= \frac{1}{2\pi} \int_{-\pi}^\pi |f(\theta)|^2 \, d\theta - \sum_{n=-N}^N \left( c_n \overline{c_n} + \overline{c_n} c_n \right) + \sum_{n=-N}^N c_n \overline{c_n} \\ &= \frac{1}{2\pi} \int_{-\pi}^\pi |f(\theta)|^2 \, d\theta - \sum_{n=-N}^N |c_n|^2. \end{align*} \]
But the left-hand side is non-negative, so we have \[ \sum_{n=-N}^N |c_n|^2 \leq \frac{1}{2\pi} \int_{-\pi}^\pi |f(\theta)|^2 \, d\theta, \] for each \(N\). Now let \(N\to \infty\). Q.E.D.

Bessel’s inequality: “\(ab\)-version”

Theorem (Bessel’s inequality — \(ab\)-version).

If \(f:\mathbb{R} \to \mathbb{C}\) is a \(2\pi\)-periodic function, integrable on \([-\pi, \pi]\), and if \(a_n\) and \(b_n\) are its Fourier coefficients, then \[ \frac{|a_0|^2}{4} + \frac{1}{2}\sum_{n=1}^\infty \left( |a_n|^2 + |b_n|^2 \right) \leq \frac{1}{2\pi} \int_{-\pi}^\pi |f(\theta)|^2 \, d\theta. \]

Riemann-Lebesgue lemma

Theorem (Riemann-Lebesgue lemma).

If \(f:\mathbb{R} \to \mathbb{C}\) is a \(2\pi\)-periodic function, integrable on \([-\pi, \pi]\), and if \(a_n\), \(b_n\), and \(c_n\) are its Fourier coefficients, then \[ \lim_{n\to \infty} a_n = \lim_{n\to \infty} b_n = \lim_{n\to \pm \infty} c_n = 0. \]