The Fourier question
Given a function \(f:\mathbb{R} \to \mathbb{R}\), when can we write it as a series of the form
\[ f(\theta) = \frac{a_0}{2} + \sum_{n=1}^\infty \left( a_n \cos{n\theta} + b_n \sin{n\theta}\right)? \]
Note we use the variable \(\theta\), rather than \(x\). No harm here.
If the answer to (2) is always, then the function \(f\) had better be periodic with period \(2\pi\), so we will focus always on these types of functions.
Recall that from Euler’s formula \(e^{i\theta} = \cos{\theta} + i\sin{\theta}\), we can express the sine and cosine functions in terms of complex exponentials as follows:
\[ \cos{\theta} = \frac{e^{i\theta} + e^{-i\theta}}{2}, \quad \sin{\theta} = \frac{e^{i\theta} - e^{-i\theta}}{2i}. \]
Express the series \[ \frac{a_0}{2} + \sum_{n=1}^\infty \left( a_n \cos{n\theta} + b_n \sin{n\theta}\right) \] in terms of complex exponentials with coefficients \(c_n\) for \(n\in \mathbb{Z}\).
Conversely, starting from the series of complex exponentials that you found in part (1), express it back in terms of sines and cosines with coefficients \(a_n\) and \(b_n\) for \(n\geq 0\).
Now, suppose we take for granted that \[ f(\theta) = \sum_{n=-\infty}^\infty c_n e^{in\theta}, \tag{1} \] and that it is permissible to integrate term-by-term. (These are assumptions, not claims of fact!)
How might we find a formula for the coefficients \(c_n\)?
Integrate both sides of (1) against \(e^{-ik\theta}\) for some fixed integer \(k\), from \(-\pi\) to \(\pi\): \[ \int_{-\pi}^\pi f(\theta) e^{-ik\theta} \, d\theta = \sum_{n=-\infty}^\infty c_n \int_{-\pi}^\pi e^{i(n-k)\theta} \, d\theta. \]
Now, compute the integrals on the right-hand side: \[ \int_{-\pi}^\pi e^{i(n-k)\theta} \, d\theta = \begin{cases} 2\pi & : n=k, \\ 0 & : n \neq k. \end{cases} \]
Therefore, we have: \[ \int_{-\pi}^\pi f(\theta) e^{-ik\theta} \, d\theta = 2\pi c_k, \] which is the same, after relabelling, as the formula \[ c_n = \frac{1}{2\pi} \int_{-\pi}^\pi f(\theta) e^{-in\theta} \, d\theta. \]
From Exercise 1, we know that \[ a_0 = 2c_0, \quad a_n = c_n + c_{-n}, \quad b_n = i(c_n - c_{-n}) \] for \(n\geq 1\).
Therefore, we can express \(a_n\) and \(b_n\) in terms of integrals of \(f\) as follows: \[ a_0 = \frac{1}{\pi} \int_{-\pi}^\pi f(\theta) \, d\theta, \quad a_n = \frac{1}{\pi} \int_{-\pi}^\pi f(\theta) \cos{n\theta} \, d\theta, \quad b_n = \frac{1}{\pi} \int_{-\pi}^\pi f(\theta) \sin{n\theta} \, d\theta, \] for \(n\geq 1\).
Definition
Let \(f:\mathbb{R} \to \mathbb{R}\) be an integrable function with period \(2\pi\).
The numbers \(c_n\) for \(n\in \mathbb{Z}\), \(a_n\) for \(n\geq 0\), and \(b_n\) for \(n\geq 1\), defined by \[ c_n = \frac{1}{2\pi} \int_{-\pi}^\pi f(\theta) e^{-in\theta} \, d\theta, \quad a_n = \frac{1}{\pi} \int_{-\pi}^\pi f(\theta) \cos{n\theta} \, d\theta, \quad b_n = \frac{1}{\pi} \int_{-\pi}^\pi f(\theta) \sin{n\theta} \, d\theta, \] are called the Fourier coefficients of \(f\).
The series \[ \sum_{n=-\infty}^\infty c_n e^{in\theta} \quad \text{or} \quad \frac{a_0}{2} + \sum_{n=1}^\infty \left( a_n \cos{n\theta} + b_n \sin{n\theta}\right) \] is called the Fourier series of \(f\).
WARNING!!!
Nothing has been claimed about the convergence of the Fourier series!
Let \(f:\mathbb{R} \to \mathbb{R}\) be an integrable function with period \(2\pi\).
If \(f\) is even, show that \(b_n=0\) for all \(n\geq 1\), and that \[ a_n = \frac{2}{\pi} \int_0^\pi f(\theta) \cos{n\theta} \, d\theta. \]
If \(f\) is odd, show that \(a_n=0\) for all \(n\geq 0\), and that \[ b_n = \frac{2}{\pi} \int_0^\pi f(\theta) \sin{n\theta} \, d\theta. \]
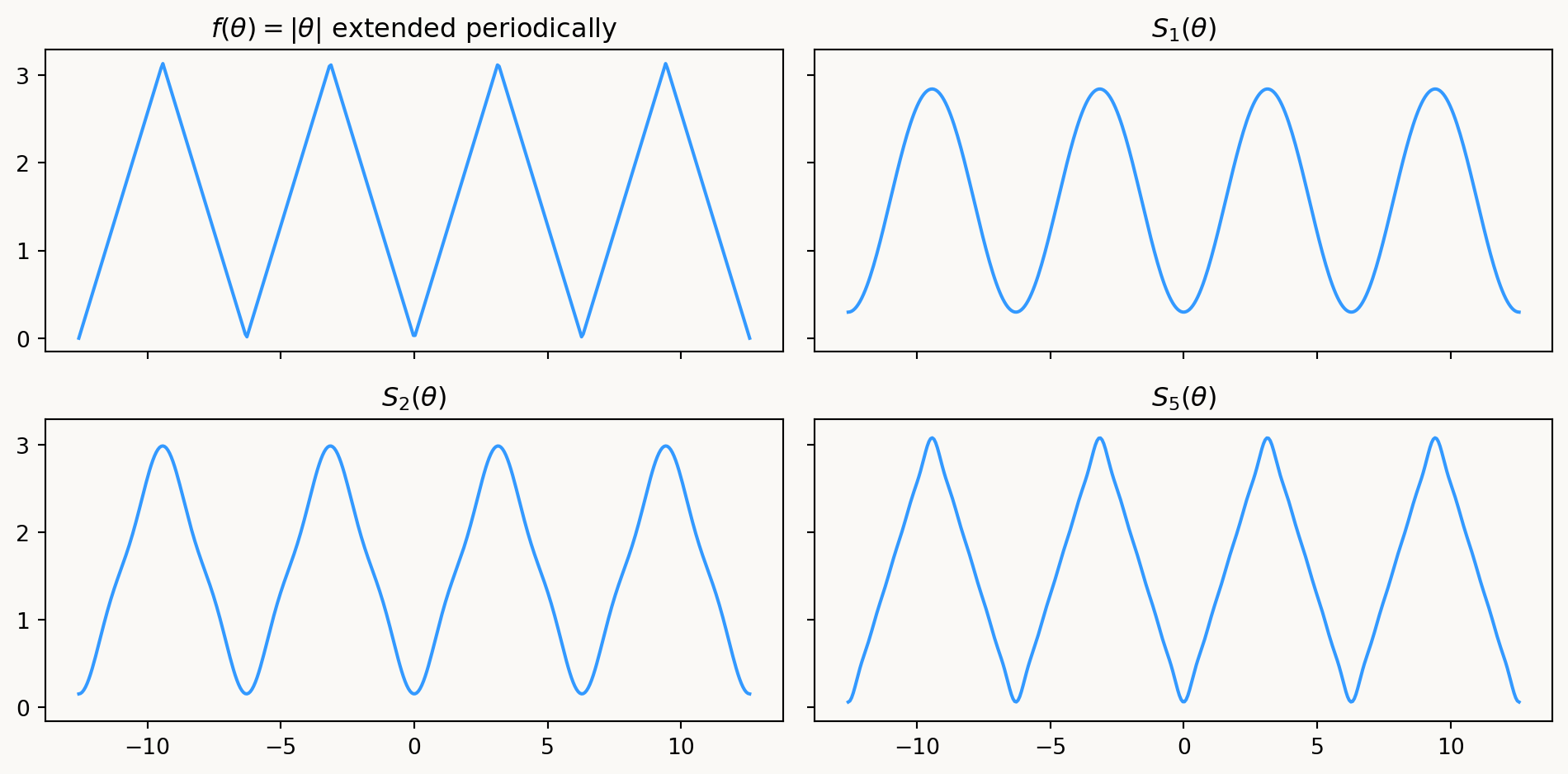
Define the function \(f(\theta) = |\theta|\) for \(\theta \in [-\pi, \pi]\), and extend it to a function on \(\mathbb{R}\) with period \(2\pi\). Compute the Fourier coefficients and series of \(f\).
