07 Functions of multiple variables, part 3

Functions as transformations

• We may try to visualize a function \(f:\mathbb{R}^m \to \mathbb{R}^n\) via its graph, as we’ve seen.

• However, we can also think of \(f\) as a physical transformation of \(\mathbb{R}^m\) into \(\mathbb{R}^n\).

• This will allow us to visualize functions all the way up to \(\mathbb{R}^3 \to \mathbb{R}^3\).

Exercise 1: Functions \(\mathbb{R} \to \mathbb{R}\) as transformations

Describe the action of the following functions \(\mathbb{R} \to \mathbb{R}\) as physical transformations of the real line into itself. Draw pictures!

1. \(f(x) = x^2\)
2. \(g(x) = 2x+1\)
3. \(h(x) = -x-1\)
4. \(k(x) = x^3\)
5. \(j(x) = \sin{x}\)

Exercise 2: Functions \(\mathbb{R} \to \mathbb{R}^2\) as transformations

Describe the action of the following functions \(\mathbb{R} \to \mathbb{R}^2\) as physical transformations of the real line into the plane. Draw pictures!

1. \(f(t) = (t, t^2)\)
2. \(g(t) = (2t+1, -t)\)
3. \(h(t) = (\cos{t}, \sin{t})\)
4. \(k(t) = (\sin{t}, \cos{t})\)
5. \(j(t) = (t^2, t^3)\)

Exercise 3: Comparison to linear functions, part 1

Compare the function \(j(t) = (t^2, t^3)\) from the previous exercise to the linear function \(L:\mathbb{R} \to \mathbb{R}^2\) defined by \(L(t) = (2t-1,3t-2)\) at the point \((1,1)\). Draw pictures!

Exercise 4: A linear function \(f:\mathbb{R}^2 \to \mathbb{R}^2\) as a transformation

Define a function \(f:\mathbb{R}^2 \to \mathbb{R}^2\) by \[ (u,v) = f(x,y) = (2x+1, x-y-1). \] Describe the action of \(f\) as a physical transformation of the plane into itself. Draw pictures!

import numpy as np
import matplotlib.pyplot as plt


blue = "#3399FF"
light_gray = "#D3D3D3"
x_range = np.linspace(-10, 10, 300)
y_range = np.linspace(-10, 10, 300)

fig, axes = plt.subplots(ncols=2, figsize=(9, 5))
fig.set_facecolor("#FAF9F6")
axes[0].set_facecolor("#FAF9F6")
axes[1].set_facecolor("#FAF9F6")

for y in np.arange(-10, 11):
    u = x_range
    v = [y] * 300
    axes[0].plot(u, v, color=blue, linewidth=1)

    axes[1].plot(u, v, color=light_gray, linewidth=0.5)

    u = 2 * x_range + 1
    v = x_range - y - 1
    axes[1].plot(u, v, color=blue, linewidth=1)


for x in np.arange(-10, 11):
    u = [x] * 300
    v = y_range
    axes[0].plot(u, v, color=blue, linewidth=1)

    axes[1].plot(u, v, color=light_gray, linewidth=0.5)

    u = [2 * x + 1] * 300
    v = x - y_range - 1
    axes[1].plot(u, v, color=blue, linewidth=1)

for ax in axes:
    ax.set_xlim(-5.9, 5.9)
    ax.set_ylim(-5.9, 5.9)

    ax.spines["top"].set_visible(False)
    ax.spines["right"].set_visible(False)
    ax.spines["bottom"].set_visible(False)
    ax.spines["left"].set_visible(False)
    ax.set_xticks([])
    ax.set_yticks([])

    ax.axhline(0, color="black", linewidth=2.5)
    ax.axvline(0, color="black", linewidth=2.5)

axes[0].text(6.15, 0, r"$x$", fontsize=14, ha="left", va="center")
axes[0].text(0, 6.15, r"$y$", fontsize=14, ha="center", va="bottom")
axes[1].text(6.15, 0, r"$u$", fontsize=14, ha="left", va="center")
axes[1].text(0, 6.15, r"$v$", fontsize=14, ha="center", va="bottom")

plt.tight_layout(w_pad=4)
plt.show()

Exercise 5: A nonlinear function \(g:\mathbb{R}^2 \to \mathbb{R}^2\) as a transformation

Define a function \(g:\mathbb{R}^2 \to \mathbb{R}^2\) by \[ (u,v) = g(x,y) = (x, x^3 + y ). \] Describe the action of \(g\) as a physical transformation of the plane into itself. Draw pictures!

fig, axes = plt.subplots(ncols=2, figsize=(9, 5))
fig.set_facecolor("#FAF9F6")
axes[0].set_facecolor("#FAF9F6")
axes[1].set_facecolor("#FAF9F6")

for y in np.arange(-10, 11):
    u = x_range
    v = [y] * 300
    axes[0].plot(u, v, color=blue, linewidth=1)

    axes[1].plot(u, v, color=light_gray, linewidth=0.5)

    u = x_range
    v = x_range**3 + y
    axes[1].plot(u, v, color=blue, linewidth=1)


for x in np.arange(-10, 11):
    u = [x] * 300
    v = y_range
    axes[0].plot(u, v, color=blue, linewidth=1)

    axes[1].plot(u, v, color=light_gray, linewidth=0.5)

    u = [x] * 300
    v = x**3 + y_range
    axes[1].plot(u, v, color=blue, linewidth=1)

for ax in axes:
    ax.set_xlim(-2.9, 2.9)
    ax.set_ylim(-2.9, 2.9)

    ax.spines["top"].set_visible(False)
    ax.spines["right"].set_visible(False)
    ax.spines["bottom"].set_visible(False)
    ax.spines["left"].set_visible(False)
    ax.set_xticks([])
    ax.set_yticks([])

    ax.axhline(0, color="black", linewidth=2.5)
    ax.axvline(0, color="black", linewidth=2.5)

axes[0].text(3.15, 0, r"$x$", fontsize=14, ha="left", va="center")
axes[0].text(0, 3.15, r"$y$", fontsize=14, ha="center", va="bottom")
axes[1].text(3.15, 0, r"$u$", fontsize=14, ha="left", va="center")
axes[1].text(0, 3.15, r"$v$", fontsize=14, ha="center", va="bottom")

plt.tight_layout(w_pad=4)
plt.show()

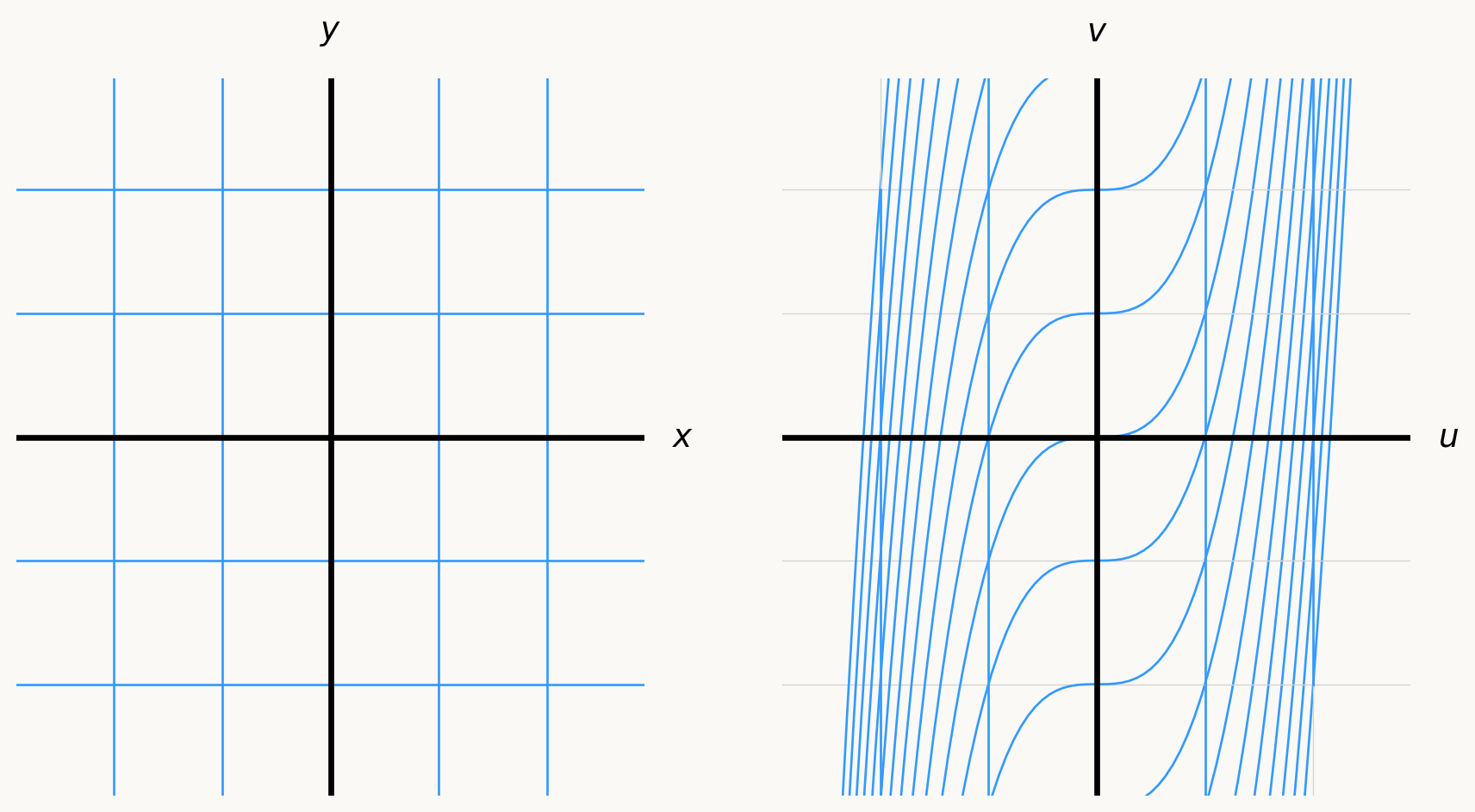
Exercise 6: A nonlinear function \(k:\mathbb{R}^2 \to \mathbb{R}^2\) as a transformation

Define a function \(k:\mathbb{R}^2 \to \mathbb{R}^2\) by \[ (u,v) = k(x,y) = (y^2 +x, y). \] Describe the action of \(k\) as a physical transformation of the plane into itself. Draw pictures!

fig, axes = plt.subplots(ncols=2, figsize=(9, 5))
fig.set_facecolor("#FAF9F6")
axes[0].set_facecolor("#FAF9F6")
axes[1].set_facecolor("#FAF9F6")

for y in np.arange(-10, 11):
    u = x_range
    v = [y] * 300
    axes[0].plot(u, v, color=blue, linewidth=1)

    axes[1].plot(u, v, color=light_gray, linewidth=0.5)

    u = y**2  + x_range
    v = [y] * 300
    axes[1].plot(u, v, color=blue, linewidth=1)


for x in np.arange(-10, 11):
    u = [x] * 300
    v = y_range
    axes[0].plot(u, v, color=blue, linewidth=1)

    axes[1].plot(u, v, color=light_gray, linewidth=0.5)

    u = y_range**2  + x
    v = y_range
    axes[1].plot(u, v, color=blue, linewidth=1)

for ax in axes:
    ax.set_xlim(-5.9, 5.9)
    ax.set_ylim(-5.9, 5.9)

    ax.spines["top"].set_visible(False)
    ax.spines["right"].set_visible(False)
    ax.spines["bottom"].set_visible(False)
    ax.spines["left"].set_visible(False)
    ax.set_xticks([])
    ax.set_yticks([])

    ax.axhline(0, color="black", linewidth=2.5)
    ax.axvline(0, color="black", linewidth=2.5)

axes[0].text(6.15, 0, r"$x$", fontsize=14, ha="left", va="center")
axes[0].text(0, 6.15, r"$y$", fontsize=14, ha="center", va="bottom")
axes[1].text(6.15, 0, r"$u$", fontsize=14, ha="left", va="center")
axes[1].text(0, 6.15, r"$v$", fontsize=14, ha="center", va="bottom")

plt.tight_layout(w_pad=4)
plt.show()

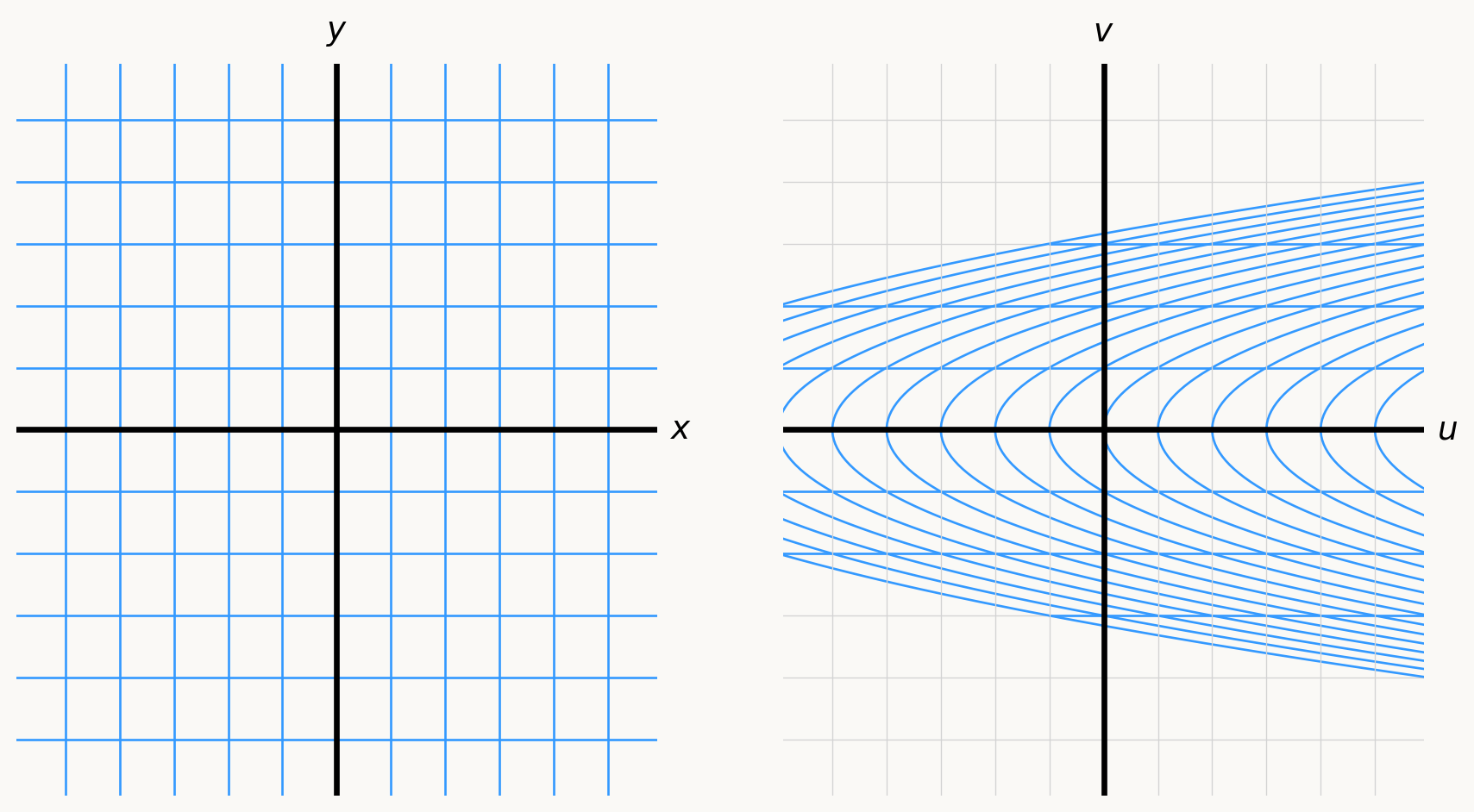
Comparison to linear functions, part 2

• Return to the function \(k(x,y) = (y^2 + x, y)\), and focus on a point in the \(xy\)-plane, say \((1,1)\), and look at its image in the \(uv\)-plane, which is \((2,1)\):

fig, axes = plt.subplots(ncols=2, figsize=(9, 5))
fig.set_facecolor("#FAF9F6")
axes[0].set_facecolor("#FAF9F6")
axes[1].set_facecolor("#FAF9F6")

for y in np.arange(-10, 11):
    u = x_range
    v = [y] * 300
    axes[0].plot(u, v, color=blue, linewidth=1)

    axes[1].plot(u, v, color=light_gray, linewidth=0.5)

    u = y**2  + x_range
    v = [y] * 300
    axes[1].plot(u, v, color=blue, linewidth=1)


for x in np.arange(-10, 11):
    u = [x] * 300
    v = y_range
    axes[0].plot(u, v, color=blue, linewidth=1)

    axes[1].plot(u, v, color=light_gray, linewidth=0.5)

    u = y_range**2  + x
    v = y_range
    axes[1].plot(u, v, color=blue, linewidth=1)

for ax in axes:
    ax.set_xlim(-3.9, 3.9)
    ax.set_ylim(-3.9, 3.9)

    ax.spines["top"].set_visible(False)
    ax.spines["right"].set_visible(False)
    ax.spines["bottom"].set_visible(False)
    ax.spines["left"].set_visible(False)
    ax.set_xticks([])
    ax.set_yticks([])

    ax.axhline(0, color="black", linewidth=2.5)
    ax.axvline(0, color="black", linewidth=2.5)

axes[0].text(4.15, 0, r"$x$", fontsize=14, ha="left", va="center")
axes[0].text(0, 4.15, r"$y$", fontsize=14, ha="center", va="bottom")
axes[1].text(4.15, 0, r"$u$", fontsize=14, ha="left", va="center")
axes[1].text(0, 4.15, r"$v$", fontsize=14, ha="center", va="bottom")

axes[0].plot(1, 1, 'ko', markersize=4) 
axes[1].plot(2, 1, 'ko', markersize=4)

plt.tight_layout(w_pad=4)
plt.show()

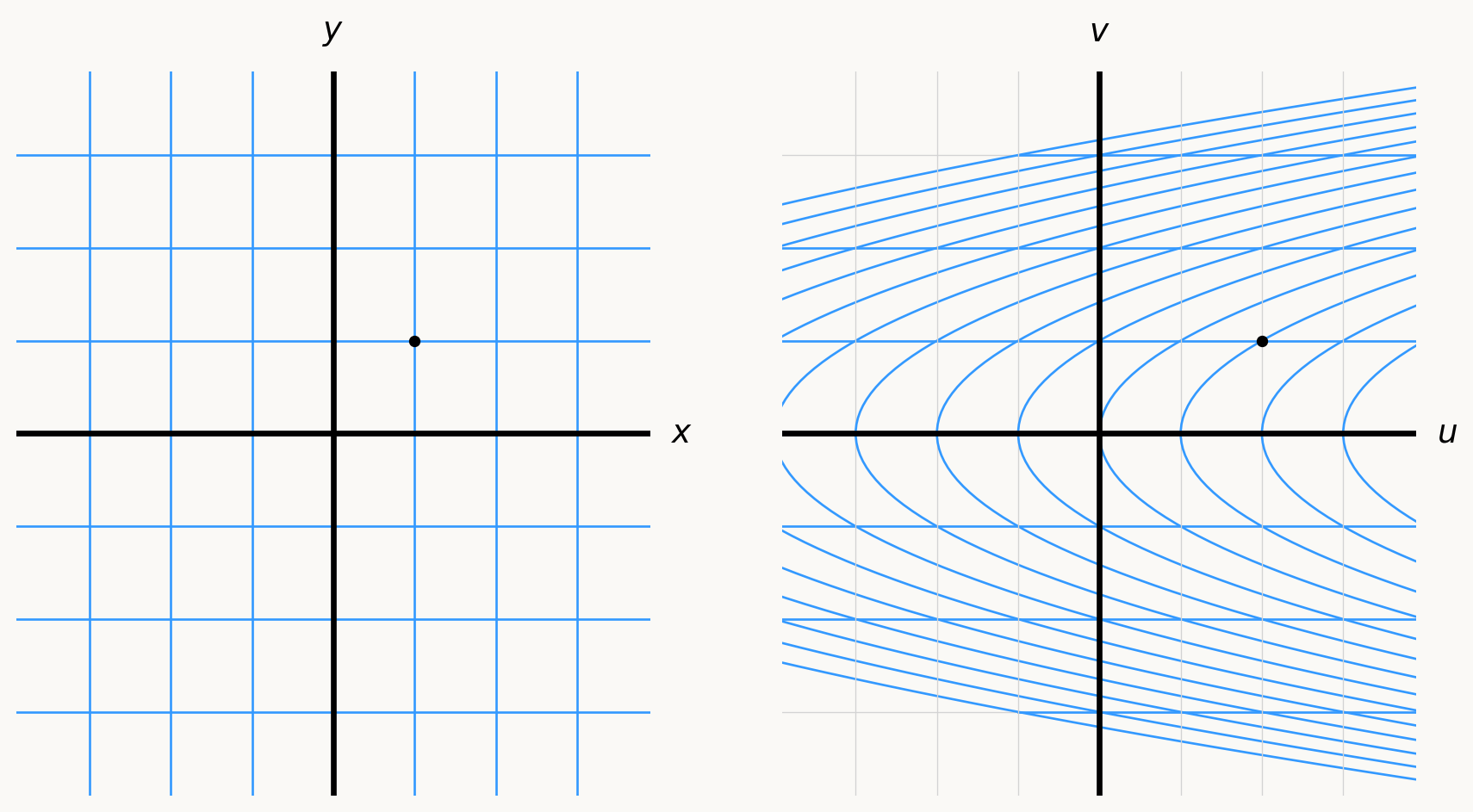
• Now consider the linear function \(L:\mathbb{R}^2 \to \mathbb{R}^2\) defined by \(L(x,y) = (x+2y-1,y)\), and focus on the same points:

fig, axes = plt.subplots(ncols=2, figsize=(9, 5))
fig.set_facecolor("#FAF9F6")
axes[0].set_facecolor("#FAF9F6")
axes[1].set_facecolor("#FAF9F6")

for y in np.arange(-10, 11):
    u = x_range
    v = [y] * 300
    axes[0].plot(u, v, color=blue, linewidth=1)

    axes[1].plot(u, v, color=light_gray, linewidth=0.5)

    u = x_range + 2 * y -1
    v = [y] * 300
    axes[1].plot(u, v, color=blue, linewidth=1)


for x in np.arange(-10, 11):
    u = [x] * 300
    v = y_range
    axes[0].plot(u, v, color=blue, linewidth=1)

    axes[1].plot(u, v, color=light_gray, linewidth=0.5)

    u = x + 2 * y_range
    v = y_range
    axes[1].plot(u, v, color=blue, linewidth=1)

for ax in axes:
    ax.set_xlim(-3.9, 3.9)
    ax.set_ylim(-3.9, 3.9)

    ax.spines["top"].set_visible(False)
    ax.spines["right"].set_visible(False)
    ax.spines["bottom"].set_visible(False)
    ax.spines["left"].set_visible(False)
    ax.set_xticks([])
    ax.set_yticks([])

    ax.axhline(0, color="black", linewidth=2.5)
    ax.axvline(0, color="black", linewidth=2.5)

axes[0].text(4.15, 0, r"$x$", fontsize=14, ha="left", va="center")
axes[0].text(0, 4.15, r"$y$", fontsize=14, ha="center", va="bottom")
axes[1].text(4.15, 0, r"$u$", fontsize=14, ha="left", va="center")
axes[1].text(0, 4.15, r"$v$", fontsize=14, ha="center", va="bottom")

axes[0].plot(1, 1, 'ko', markersize=4) 
axes[1].plot(2, 1, 'ko', markersize=4)

plt.tight_layout(w_pad=4)
plt.show()

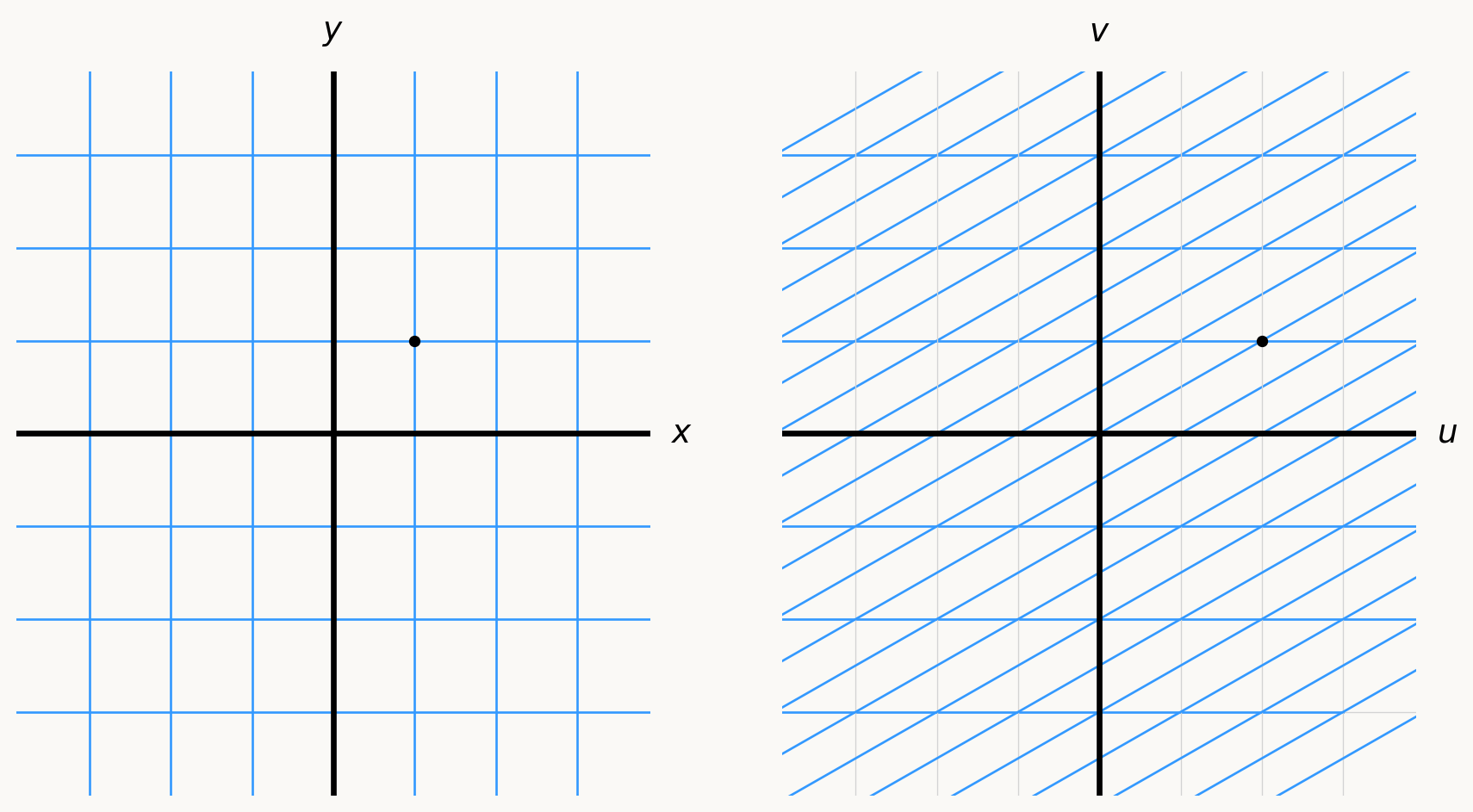
• Do you notice how that, if you only compare the graphs in the \(uv\)-plane near the point \((2,1)\), the function \(k\) looks a lot like the linear function \(L\)? That’s because \(L\) is the “best” linear approximation of \(k\) near \((1,1)\), cooked up using the derivative of \(k\) at \((1,1)\).

• Same story here as in single-variable calculus. Nothing new conceptually.