06 Functions of multiple variables, part 2

More plotting strategies for graphs

Strategies for plotting graphs of \(f: \mathbb{R}^2 \to \mathbb{R}\)

1. Intersect the graph with horizontal planes of the form \(z=c\), for various values of \(c\).
   • The equation you solve is \(c = f(x,y)\).
   • These cross sections (also called level sets!) are curves in the \(xy\)-plane.
2. Intersect the graph with vertical planes of the form \(x=c\), for various values of \(c\).
   • The equation you solve is \(z=f(c,y)\).
   • These cross sections are curves in the \(yz\)-plane.
3. Intersect the graph with vertical planes of the form \(y=c\), for various values of \(c\).
   • The equation you solve is \(z=f(x,c)\).
   • These cross sections are curves in the \(xz\)-plane.

Exercise 1: Practice with cross sections

Plot the graphs of the following functions by using cross sections.

1. \(f(x,y) = x^2 - y^2\)
2. \(g(x,y) = y\sin{x}\)
3. \(h(x,y) = -2x - y +5\)
4. \(k(x,y) = y^3 + xy\)

Contour plots

Placing all of the level sets of a function \(f:\mathbb{R}^2 \to \mathbb{R}\) in the \(xy\)-plane gives us a contour plot of \(f\).

• So, a contour plot is like a topographic map of the graph of \(f\).
• In this context, the level sets are often called contours or contour lines.

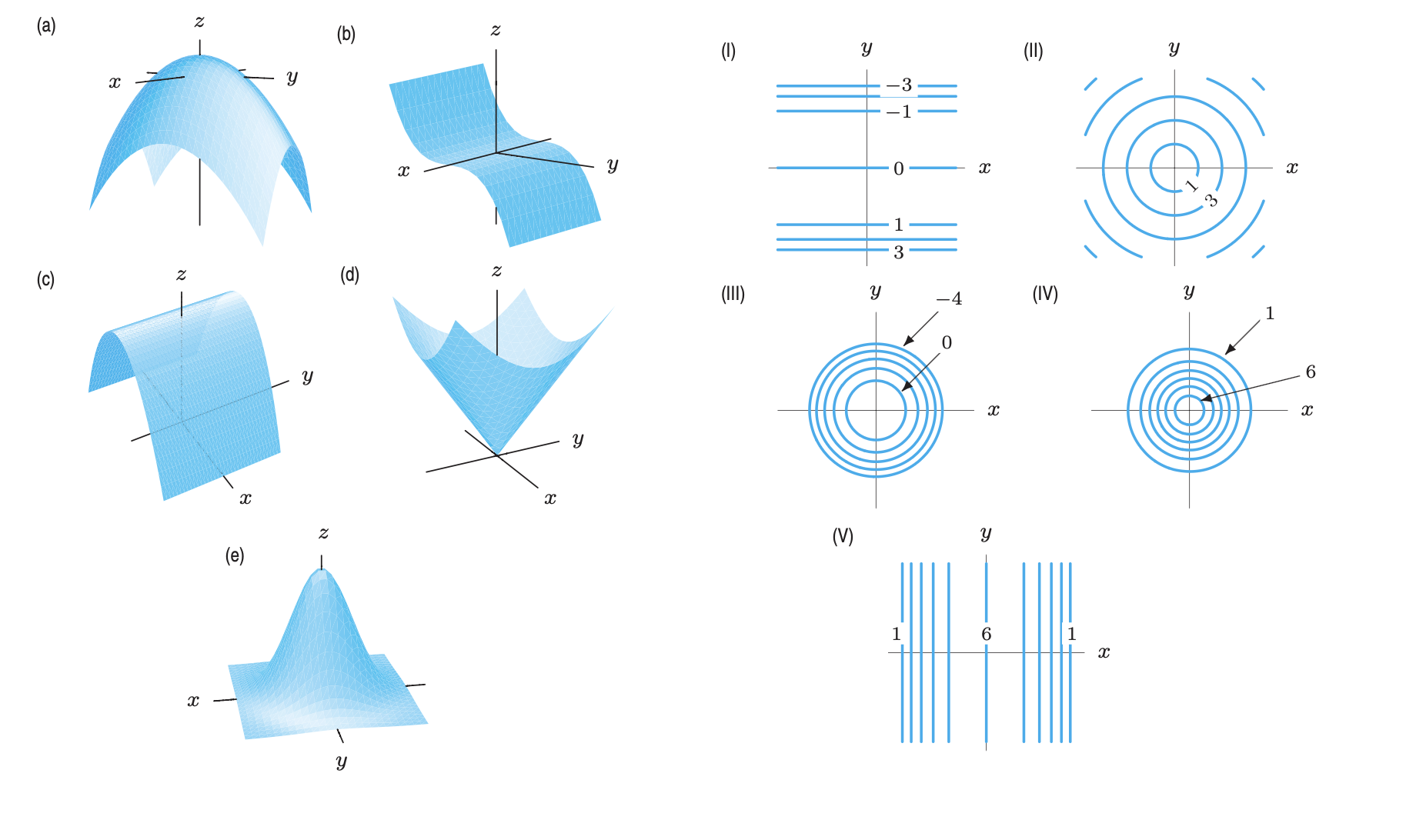
Exercise 2: Matching contour plots

Match the graphs to the contour plots.

Exercise 3: Sketch a contour plot

Sketch a contour plot for the function \(f(x,y) = xy\).